티스토리 뷰
Stack 사용
#include <iostream>
#include <vector>
#include <stack>
using namespace std;
vector<int> edge[10];
bool mark[10];
void dfs(int n) {
stack<int> s;
s.push(n);
mark[n] = true;
cout << n << ' ';
while(!s.empty()) {
int f = s.top();
bool none = true;
for(int x : edge[f]) { // 정점에 연결된 모든 간선 탐색
if(!mark[x]) {
s.push(x);
mark[x] = true;
cout << x << ' ';
none = false;
break;
}
}
// none이 true면 그래프에서 더이상 진행할곳이 없음
// 현재 정점에서 이어진 곳이 모두 이미 방분됨.
if(none) s.pop();
}
}
int main() {
int v, e; // vertex, edge
cin >> v >> e;
for(int i = 0; i < e; i++) {
int f, t;
cin >> f >> t;
edge[f].push_back(t);
edge[t].push_back(f);
}
dfs(1);
}
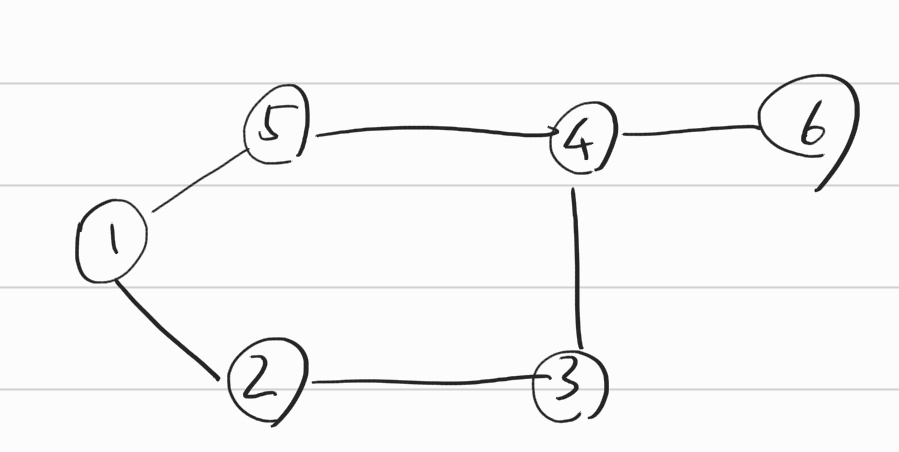
input:
6 8 // vertex, edge
1 2
1 5
2 3
2 4
2 5
3 4
4 5
4 6

재귀 사용
#include <iostream>
#include <vector>
using namespace std;
vector<int> edge[10];
bool mark[10];
void dfs(int n, int from) {
if(mark[n]) {
cout << "I'm from: " << from << ", n is: " << n << ". return" << '\n';
return;
}
mark[n] = true;
cout << "im from: "<< from << ", n is: " << n << '\n';
for(int x : edge[n]) { dfs(x,n); }
}
int main() {
int v, e;
cin >> v >> e;
for(int i = 0; i < e; i++) {
int f, t;
cin >> f >> t;
edge[f].push_back(t);
edge[t].push_back(f);
}
dfs(1,1);
}
결과:

지금까지 별 생각 없이 재귀를 사용하고 있었는데, 재귀가 dfs랑 상당히 비슷하게 작동한다는 것을 배울수 있었다.
재귀함수가 실행될때, 예를들어 2번 정점을 검토할때, 1은 이미 방문했으므로 리턴되고, 3은 아직 방문하지 않았으므로 dfs(3)이 실행되는데,
이때 edge[2]에 아직 4와 5가 남아있다.
이때 dfs(3)이 먼저 실행되고(그 안에서 재귀함수들이 또 쭉 호출된다), 그 이후 돌아와서 dfs(4), dfs(5)가 호출된다.
즉 재귀가 dfs 그 자체처럼 하나의 요소를 쭉 파고들고 다시 돌아오는 방식으로 작동된다.
'알고리즘' 카테고리의 다른 글
| c++) Floyd Warshall (0) | 2021.12.28 |
|---|---|
| bfs 탐색 깊이 기록하기 (0) | 2021.07.19 |
| Recursion (재귀) (0) | 2021.07.15 |
| DFS를 이용한 조합 만들기 (0) | 2021.07.12 |
| BFS (0) | 2021.03.17 |
댓글
공지사항
최근에 올라온 글
최근에 달린 댓글
- Total
- Today
- Yesterday
링크
TAG
- Python
- dfs
- Brute Force
- Spring
- priority queue
- DP
- MVC
- CSS
- BFS
- two pointer
- Implementation
- Unity
- 재귀
- 조합
- 자료구조
- permutation
- recursion
- C++
- binary search
- floyd warshall
- Stack
- 이분탐색
- Dijkstra
- graph
- Kruskal
- back tracking
- C
- db
- greedy
- Tree
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
글 보관함
