티스토리 뷰
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
vector<int> edge[10];
bool mark[10];
void bfs(int idx)
{
// {방문 정점, 깊이}
queue<pair<int,int>> q;
// 정점 idx, 시작 정점이므로 깊이는 0부터 시작
q.push({idx, 0});
// 방문 기록
mark[idx] = true;
while(!q.empty())
{
// 기준 정점
int vertex = q.front().first;
// 깊이
int depth = q.front().second;
q.pop();
cout << "depth: " << depth << endl;
cout << "vertex: " << vertex << endl;
// 기준 정점과 이어져 있는 모든 정점들 탐색
for(auto x : edge[vertex])
{
// 기준 정점과 이어져있지만 이미 방문했다면 continue
if(mark[x]) continue;
mark[x] = true;
// 이어진 정점과 깊이를 큐에 푸쉬
q.push({x, depth+1});
}
}
}
int main()
{
int v, e;
cin >> v >> e;
for(int i = 0; i < e; i++)
{
int f,t;
cin >> f >> t;
edge[f].push_back(t);
edge[t].push_back(f);
}
bfs(0);
}
input:
6 6. // 정점, 간선 갯수
0 1 // 서로 이어진 정점들
1 2
0 4
0 2
2 3
4 5
output:
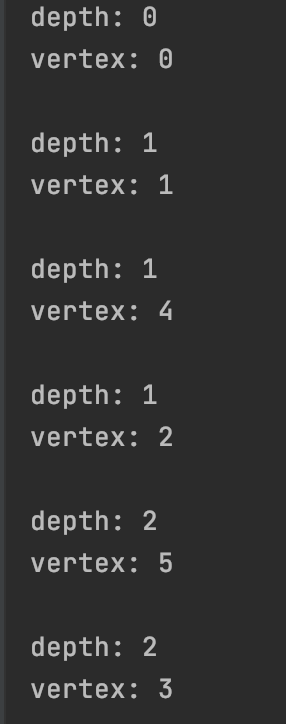
'알고리즘' 카테고리의 다른 글
| 최소 신장 트리(MST), 크루스칼 알고리즘 (kruskal) (0) | 2022.01.18 |
|---|---|
| c++) Floyd Warshall (0) | 2021.12.28 |
| Recursion (재귀) (0) | 2021.07.15 |
| DFS를 이용한 조합 만들기 (0) | 2021.07.12 |
| BFS (0) | 2021.03.17 |
댓글
공지사항
최근에 올라온 글
최근에 달린 댓글
- Total
- Today
- Yesterday
링크
TAG
- binary search
- 자료구조
- 재귀
- Implementation
- 조합
- priority queue
- dfs
- floyd warshall
- two pointer
- Spring
- Brute Force
- recursion
- back tracking
- C
- db
- MVC
- Python
- permutation
- Tree
- C++
- CSS
- Dijkstra
- DP
- Unity
- Stack
- Kruskal
- BFS
- graph
- greedy
- 이분탐색
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
글 보관함
