티스토리 뷰
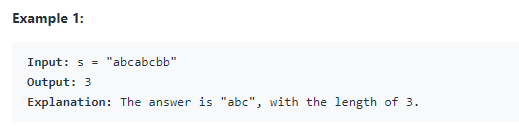
"abcabcbb"
int left = 0, right = 0;
for(right = 0; right < s.size(); right++) {
a // l = 0, right = 0
ab // l = 0, right = 1
abc // l = 0, right = 2
// 다음이 a인데 a는 이미 있다. 따라서 left를 전에 있던 a다음으로 옮김.
bc // l = 1, r = 2
bca // l = 1, r = 3
// 다음은 b인데 b는 이미 있다. 따라서 left를 전에 있던 b 다음으로 옮김
ca // l = 2, r = 3
cab // l = 2, r = 4
// 다음은 c인데 c는 이미 있다. 따라서 left를 전에 있던 c 다음으로 옮김.
ab // l = 3, r = 4
abc // l =3, r = 5
// 다음은 b인데 b는 이미 있다. 따라서 left를 전에 있던 b 다음으로 옮김.
c // l = 5, r = 5
cb // l = 5, r = 6
// 다음은 b인데 b는 이미 있다. 따라서 left를 전에 있던 b 다음으로 옮김.
b // l = 7, r = 7
이미 있는 문자인지 아닌지를 구분하는것은 map<char, int>를 이용.
if(map.find(s[right]) != map.end()) { // 이말은 map에 현재 찾는 문자가 이미 있다는것.
left = max(left, dict[s[right]] + 1); // 이말은 left를 전에 있던 중복문자 다음으로 옮긴다는 것.
}
즉 map<char, int>는 문자들의 가장 최신 위치를 나타낸다고 할수있다.
map<char,int> map = { {a,3}, {b,4}, {c,2} }
라면, "abcabcbb"에서 가장 최근 위치가 a는 s[3], b는 s[4], c는 [2].
따라서 map을 이용해서 중복문자인지 찾고, left값이 계속 그 다음으로 이동.
#include <iostream>
using namespace std;
#include <map>
int lengthOfLongestSubstring(string s) {
int left = 0, len = 0;
/// 중복문자의 가장 최신 위치를 나타낸다고 할수있음.
map<char, int> map;
for(int right = 0; right < s.size(); right++) {
if(map.find(s[right]) != map.end()) { /// dict에 현재 찾는 문자가 존재하면
/// dict에 중복되는 문자가 있으면, 그 중복되는 문자 다음으로 left가 이동.
/// 그 전은 생각할 필요없다. 왜? 중복되는 문자는 substring에 있을수 없으므로.
left = max(left, map[s[right]] + 1); /// 이말은 left를 전에 있던 중복문자 다음으로 옮긴다는 것.
}
map[s[right]] = right; /// 중복문자 위치 갱신
len = max(len,right - left + 1); /// len 갱신
}
return len;
}
int main() {
string s = "";
int len;
len = lengthOfLongestSubstring(s);
cout << len;
}'PS' 카테고리의 다른 글
| leetcode) #53. Maximum Subarray (0) | 2021.02.22 |
|---|---|
| leetcode) #20) Valid Parentheses (0) | 2021.02.22 |
| leetcode) #1. Two sum (0) | 2021.02.18 |
| leetcode와 백준 (0) | 2021.02.17 |
| 14888. 연산자 끼워넣기 (0) | 2020.10.01 |
- Total
- Today
- Yesterday
- Python
- floyd warshall
- 조합
- two pointer
- priority queue
- DP
- Spring
- Unity
- Dijkstra
- permutation
- C
- CSS
- recursion
- Stack
- Implementation
- back tracking
- Tree
- greedy
- Brute Force
- BFS
- binary search
- 재귀
- 자료구조
- MVC
- Kruskal
- C++
- 이분탐색
- dfs
- graph
- db
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
