티스토리 뷰
https://www.acmicpc.net/problem/11054
11054번: 가장 긴 바이토닉 부분 수열
첫째 줄에 수열 A의 크기 N이 주어지고, 둘째 줄에는 수열 A를 이루고 있는 Ai가 주어진다. (1 ≤ N ≤ 1,000, 1 ≤ Ai ≤ 1,000)
www.acmicpc.net
바이토닉 부분수열이란, 수열 S가 어떤 수 Sk를 기준으로 S1 < S2 < ... Sk-1 < Sk > Sk+1 > ... SN-1 > SN을 만족하는 수열이다. 즉 여러번의 증가와 감소가 나타나지 않는 수열이다.
예를들어 {10,20,30,25,20}. 그리고 {10,20,30,40}, {50,40,25,10}처럼 한번의 증가 or 감소만 있어도 바이토닉 부분수열이다.
{1, 2, 3, 2, 1, 2, 3, 2, 1}과 {10, 20, 30, 40, 20, 30} 처럼 여러번의 증가,감소가 있으면 바이토닉 부분수열이 아니다.
처음에 이 문제를 푼 방식은 그냥 수열의 처음부터 가장 큰 수까지의 길이와 그 다음부터 감소하는 수의 길이를 더해서 풀었다. 제출했는데 계속 틀렸다고 나왔고 예외도 찾지 못하고, 내가봐도 코드가 별로였다..
코드
import sys
n = int(input())
d = [1] * n # 기록할 배열
a = [0] * n # 수열 저장할 배열
a = input().split()
if n == 1: # 길이가 1이면 1일수 밖에없음
print(0)
sys.exit()
for i in range(n): # str로 입력한 배열들 int로 변경
a[i] = int(a[i])
"""
일단 수열 처음부터 끝까지 증가수열 체크
증가수열 중 가장 큰 수의 idx를 max_d에 저장
"""
max_length = 0
max_d = 0
for i in range(n):
length = 0
trigger = 0
for j in range(i):
if a[j] < a[i]:
length = max(d[j], length)
d[i] = length + 1
if max_length < d[i]:
max_length = d[i]
trigger = 1
if trigger == 1:
max_d = i
no_rise = 0
if max_length == 1: # 증가수열 해당없으면
max_d = 0
max_length = 0
no_rise = 1 # 증가수열이 없다!
for i in range(max_d, n, 1): # 증가수열 뒤 1로 모두 초기화
d[i] = 1
"""
max_d부터 감소수열 체크
증가수열 검사할때 가장 큰 수였던 a[max_d]는 제외하고 체크해야함
"""
max_length2 = 0
max_d2 = 0
for i in range(max_d, n, 1):
if a[i] >= a[max_d] and no_rise == 0:
d[i] = 0
continue
length2 = 0
trigger2 = 0
for j in range(max_d, i, 1):
if a[j] > a[i]:
length2 = max(d[j], length2)
d[i] = length2 + 1
if max_length2 < d[i]:
max_length2 = d[i]
trigger2 = 1
if trigger2 == 1:
max_d2 = i
print(max_length + max_length2)
Solution
솔루션을 보니 전에 푼 가장 긴 증가하는 부분수열, 가장 긴 감소하는 부분수열의 알고리즘을 이용했다.
바로 전에 이 문제들을 풀었는데 왜 저걸 이용할 생각을 못했는지 모르겠다.
일단 가장 긴 증가하는 부분수열 문제에서처럼 수열의 가장 긴 증가하는 부분수열의 길이를 구한다.
그리고 뒤에서부터 또 가장 긴 증가하는 부분수열의 길이를 구한다. 그럼 뒤에서 부터 구했으니 감소하는 부분수열이 된다.
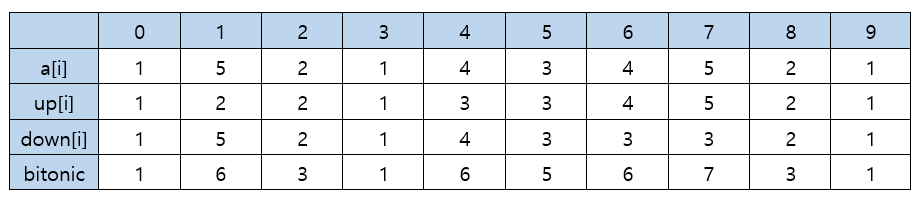
그러면 가장 긴 바이토닉 부분수열을 구하는 방법은?
up배열 의 수 와 down 배열 의 수를 더해서 가장 큰 수에서 1을 뺀것이 답이다.
예를들어 위 예제 에서는 답이 i = 7에서 5 + 3 - 1해서 답은 7이다. 즉 가장 긴 바이토닉 부분수열의 길이가 7이다.
i = 7을 보자.
일단 앞에서 부터 증가인 up을 보면 수열은 {1, 5, 2, 1, 4, 3, 4, 5} 이고 증가수열은 {1, 2, 3, 4, 5}로 길이는 5이다.
뒤에서 부터 증가 즉 감소인 down을 보면 수열은 {5, 2, 1}이고 감소수열은 {5, 2, 1}로 길이는 3이다.
이 두 수열을 합하면 {1, 2, 3, 4, 5, 5, 2, 1}이다. 그런데 이때 가장 큰 수인 5가 중복되므로 1을 빼는것이다.
즉 가장 긴 바이토닉 수열은 {1, 2, 3, 4, 5, 2, 1}이고 길이는 7이된다.
up = [0] * 1001
dn = [0] * 1001
n = int(input())
a = input().split()
for i in range(n): a[i] = int(a[i])
# 앞에서 부터 증가수열 탐색
for i in range(n):
up[i] = 1
for j in range(i):
if a[j] < a[i]: up[i] = max(up[i], up[j] + 1)
# 뒤에서 부터 증가수열 탐색 (앞에서 보면 감소수열)
for i in range(n-1, -1, -1):
dn[i] = 1
for j in range(i+1, n):
if a[j] < a[i]: dn[i] = max(dn[i], dn[j] + 1)
res = 0
for i in range(n):
res = max(res, up[i] + dn[i] - 1)
print(res)
'PS' 카테고리의 다른 글
| 1912. 연속합 (0) | 2020.08.11 |
|---|---|
| 11055. 가장 큰 증가 부분 수열 (0) | 2020.08.11 |
| 11722. 가장 긴 감소하는 부분수열 (0) | 2020.08.10 |
| 11053. 가장 긴 증가하는 부분수열 (0) | 2020.08.10 |
| 9465. 스티커 (0) | 2020.08.10 |
- Total
- Today
- Yesterday
- 자료구조
- Brute Force
- MVC
- Stack
- binary search
- permutation
- C++
- DP
- db
- 조합
- priority queue
- BFS
- dfs
- 재귀
- greedy
- floyd warshall
- 이분탐색
- Tree
- back tracking
- C
- Kruskal
- Implementation
- Python
- two pointer
- Dijkstra
- recursion
- Unity
- CSS
- Spring
- graph
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
